...how fitting two 9g servos in the wrong place could add another 135g to your plane's weight.
It's all to do with an engineering principle called MOMENTS.
See it here in the common-sense problem of how three kids of equal weight can still play on a see-saw.
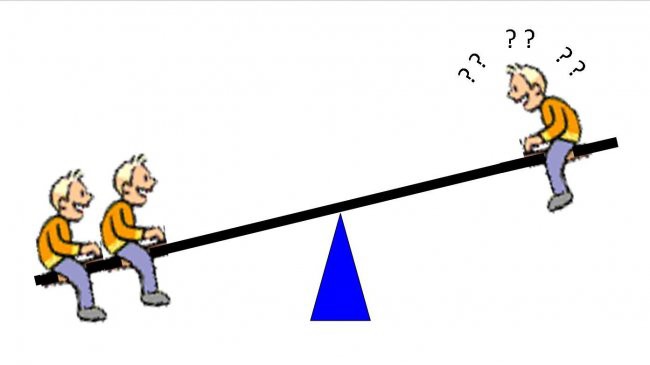
If the two kids sit the same distance out from the balance point (fulcrum) as the single kid, they will tip the see-saw in their direction. The single kid can jump about as much as he likes, but there's no way he can lift the two kids off the ground. That's no fun!
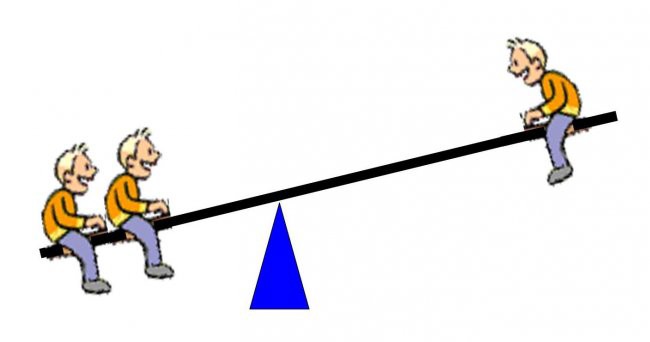
If the fulcrum is moved closer to the two kids, eventually it reaches a point where the see-saw balances and they can all play.
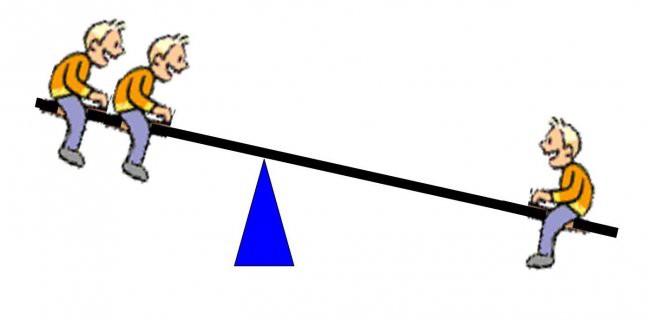
In fact the distance from the fulcrum that the two kids sit at will be exactly half the distance from the fulcrum as the single kid is sitting at.
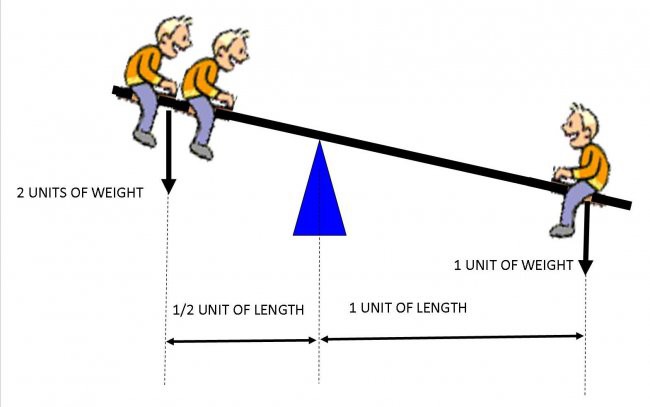
In simple terms;
two kid weights x half a unit of length = one kid weight x one unit of length
In engineering terms;
force x distance = force x distance
For the system (kids on a see-saw) to be in equilibrium (balanced) the final numbers on either side of the equals sign must be the same;
2 x ½ = 1 x 1
This means that the shorter the distance to the balance point, the more weight is needed to achieve balance – equally the further a weight is from the balance point the more effect it has. Now let's see how we can use that knowledge inour scratch build planes.
So you have a model of a snub-nosed plane like a Bristol M.1
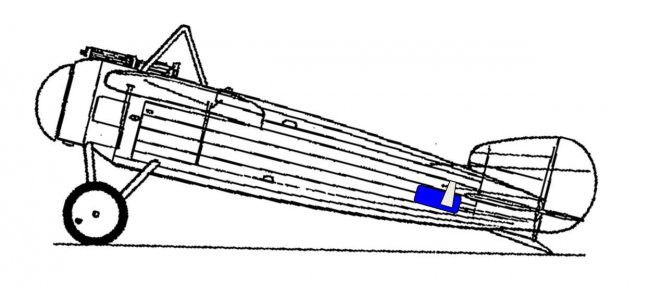
You add two 9g servos (18g) to the tail and, no surprise, the plane becomes tail heavy.
If the only place to add balance weight is 40mm forward from the CG - how much weight do you need to add to make it balance?
If we know the servos are 300mm from the CG we can use the principle of moments rule;
force x distance = force x distance
[This works equally well for inches and ozs – as long as the units used on either side of the equals sign are consistent.]
Sticking in the numbers;
balance weight (grams) x 40mm = 18g x 300mm
balance weight x 40 = 5400
balance weight = 5400/40
balance weight = 135 grams
So we need to add 135 grams at the nose to get the plane to balance.
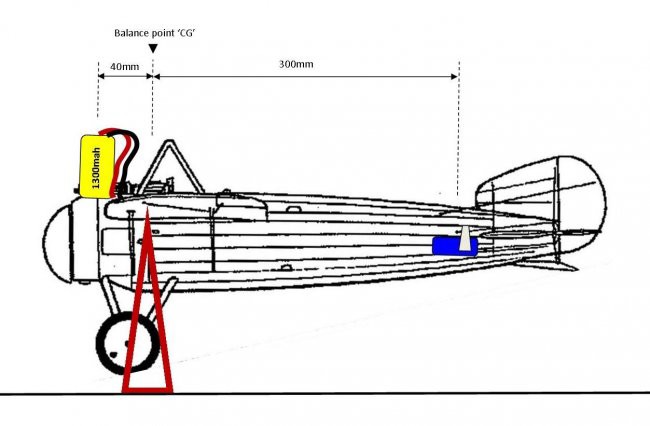
135 grams could be the weight of a 3S 1300mah LiPo, but you'd never get it to fit at the right distance away from the CG to completely balance the weight of the servos.
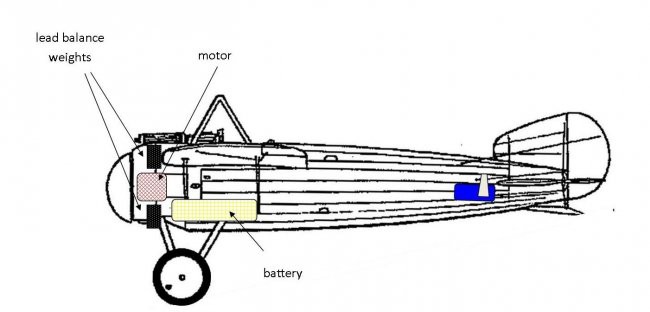
Much more likely is that the battery, say about 500mah for this plane, will fit neatly in a compartment under the fuselage; but as it sits either side of the CG it's effect on the balance will be much less than the 135g needed. It might even have little or no effect on balance - which means you still need to add 135g of lead to the firewall to get the plane to balance. 135g of dead weight!
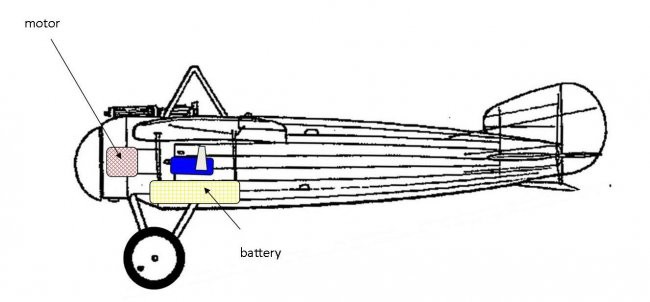
If you'd mounted the servos under the wing at the CG point you avoid the need for balance weights and avoid adding a whole pile of unnecessary weight to the plane.
Of course that's a worst case scenario. Sometimes fitting the servos near the rear is fine as they do the job of balancing out battery and fuselage weight, but I'm surprised how many people show off models with rear-mounted servos and then say they had to add a pile ofweight at the front to get the plane to balance.
Deciding where to put things can be tricky, but as a general rule avoid putting weight on the tail unless you know for sure that it's needed to achieve the final balance.